¶ Power
<THIS SECTION IS UNDER CONSTRUTION>
¶ General concepts
This section describes the general concepts of power we apply to power the Smart Parks Infrastructure. Many concepts we describe here will be presented in simplified form. For our users this section is more used as a quick reference. We encourage to find more extensive resources and documentation on this topic that suits your level of understanding.
We have found that a very helpful source of information is this wiki from The Stanford Center for Computer Research in Music and Acoustics (CCRMA) → https://ccrma.stanford.edu/wiki/Introduction_to_Electronics
¶ Electrical Circuit
To power any of the elements in the Smart Parks infrastructure we make use of electrical circuits and all concepts that come with it. An interconnection of electrical elements that contains a closed loop is an electrical circuit. The closed loop allows electrons to flow through the electrical elements.
We now explain how to analyze simple electrical circuits in terms of voltage, current, and resistance.
¶ Current, Voltage, Resistance
- Current (I) → describes the quantity of electrons passing through a point in a circuit at a given instant in time. Current is measured in Amperes (Amps, A).
- Voltage (V) → describes the potential difference in electrical charge between two points in an electrical circuit. Voltage (also known as electric potential) is measured in Volts (V).
- Resistance (R) → (a special case of Impedance) describes the capacity of a circuit element to resist or impede the flow of electrons in the circuit. Resistance in measured in Ohms (Ω).
A common analogy may be used to relate these three quantities to water flow in pipes in place of electrons in wires. Imagine you have two water tanks connected from the bottoms by a pipe (such as the drain of a double sink). If one tank is full of water and the other one nearly empty we know intuitively that the water in the full tank will flow through the pipe into the nearly empty tank. Current (I) is analogous to the quantity of water flowing through a pipe at a given moment in time.
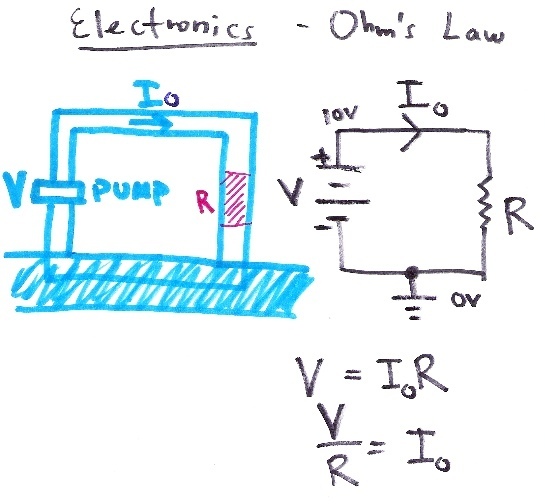
¶ Ohm's law
When we are working with electric power within the Smart Parks Infrastructure we often use the Ohm's law.
Ohm's law states that the current through a conductor between two points is directly proportional to the voltage across the two points.
To use this law in practice, we need to take a look at the main equation:
- V = IR Ohm's Law states that Voltage = Current x Resistance or V = IR. The equation can be rearranged to find any one of the three quantities given the other two.
Example:
Consider the following circuit:
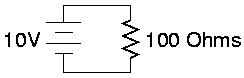
The voltage in the circuit is given as 10V from the battery and the resistance is also given as the 100 ohm resistor is the only resistive element in the circuit. So now we can compute the current in the circuit as:
- I = V/R → 10V / 100 Ohms → 0.1 Amps
¶ Calculating Power
Calculating the power dissipated by a circuit element is simple. Often much of this power is converted into heat, so by thinking about the power dissipated by circuit elements, you can make sure that they don't burn up or catch on fire!
- Power (in Watts) = Voltage (in Volts) x Current (in Amps) → P = V I
Combining with Ohm's law we get two other useful forms:
- P = V*V / R
- P = I*I*R
Power is a measurement of the amount of work that can be done with the circuit, such as lighting a light bulb or powering a LoRaWAN gateway.
Example:
Consider a 100 Watt light bulb in your home. We know the voltage applied to the bulb is normally 110V or 220V, so we can calculate the current consumed as follows:
- I = P/V = 100W / 110V = 0.91 Amps
- I = P/V = 100W / 220V = 0.45 Amps
So you can see why using a 60 Watt light bulb is more economical. Your electric company normally charges you for your usage in Killo-Watt Hours (kWh). One kWh is the amount of energy necessary to do 1000 Watts of energy for one hour - in other words to keep 10 100W light bulbs shining for one hour.
Now consider a LoRaWAN Gateway that uses 5 Watt, that needs to be powered by a battery. For simplicity we take a 12V and a 24V battery, so we can calculated the current consumed as follows:
- I = P/V = 5W / 12V = 0.416 Amps
- I = P/V = 5W / 24V = 0.208 Amps
So you can see why using a higher voltage battery system in this circuit reduces the Current. An important difference between the example with the light bulb and the LoRaWAN gateway, is the type of current used. The light bulb example uses power from the main grid and if the type Alternating Current (AC). The LoRaWAN gateway example is using a battery to power the gateway and therefore uses Direct Current (DC). You can see that the difference does not have an impact on calculating the power and using Ohm;s law. However, the difference is very important in building circuits. Therefore, these concepts are explained in more detail below.
¶ AC / DC
Explain difference in AC and DC:
- Alternating Current → AC → In alternating current (AC) systems, the movement of electric charge periodically reverses direction. AC is the form of electric power most commonly delivered to businesses and residences. The usual waveform of an AC power circuit is a sine wave, though certain applications use alternative waveforms, such as triangular or square waves.
- Direct Current → DC → In contrast, direct current (DC) refers to a system in which the movement of electric charge in only one direction (sometimes called unidirectional flow). Direct current is produced by sources such as batteries, thermocouples, solar cells, and commutator-type electric machines of the dynamo type.
Conversion between AC and DC:
- AC to DC: Alternating current can also be converted to direct current through use of a rectifier. In general these rectifiers are called “adapters” which come with many modern devices like smartphones and computers. These devices internally run on DC, but can be charged or powered via the mains (which is AC) with the use of an adapter.
- DC to AC: Direct current can also be converted to alternating current through use of an inverter. We find these inverters in places where the appliance usually can only be powered by AC but operates in a battery powered environment (which is DC).
We have to understand that the conversion between AC and DC always comes with the loss of power. Therefore it is wise to prevent this conversion. Especially in situations of extreme power scarcity.
If you like this topic we strongly advice you to read about the “War of the Currents”.
¶ Series versus Parallel
Working with DC electrical circuits, we often connect batteries and solar panels in different configurations called Series and Parallel. In order to understand how these configurations impact our circuit, need to look at Kirchhoff's Voltage and Kirchhoff's Current Law.
Kirchhoff's Voltage Law: The sum of the voltages around any closed circuit must be zero." An important consequence is that the voltage across each branch in a circuit is the same. This explains why the voltages across the battery and across the resistor in the above circuit are the same. Here are important consequences of Kirchhoff's Voltage Law. See if you can derive them:
- Voltages sum in series.
- Electrical components placed in series all share the same current.
Kirchhoff's Current Law: the sum of the currents entering a node must equal the sum of the currents leaving a node. This law is a consequence of the conservation of charge (electrons) in electrical networks. Here are some important consequences of Kirchhoff's Current Law. See if you can derive them:
- Currents sum in parallel.
- The ends of electrical components connected by a wire all share the same voltage.
Example:
The best way to show the impact of these laws onto our installations is to consider the following two examples:
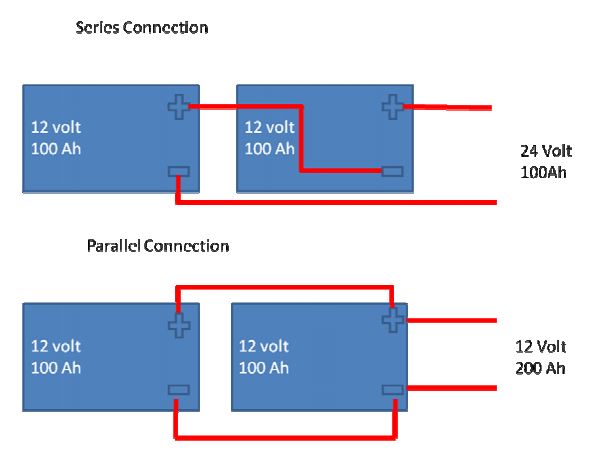
- Series Circuits
- Batteries: 2 x 12V @ 100Ah batteries in series will provide 24V - 100Ah
- Solar Panels: 2 x 38V @ 300Wp solar panels in series will provide 76V @ 300Wp
- Parallel Circuits
- Batteries: 2 x 12V @ 100Ah batteries in parallel will provide 12V - 200Ah
- Solar Panels: 2 x 38V @ 300Wp solar panels in parallel will provide 38V @ 600Wp
¶ Power consumption
To estimate the power consumption for parts of the Smart Parks Infrastructure, one need to look at the individual elements. We will provide a list of known power consumption per device for the purpose of helping to design an adequate power setup. The given numbers are not very precise and are more based on our own experience, but should be enough to serve the purpose.
LoRaWAN Gateways
- Kerlink iBTS → 10W
- Kerlink iStation → 5.5W
- Kerlink Station → 3W
- Mikrotik wAP LR8/9 → 5W
- Mirkotik LtAP LR8/9 LTE → 5W
- Larank8 → 5W
IP Backbone
- Ubiquity EdgeSwitch ES-8 150W → 5W (+ the power it needs to provide over PoE)
- Ubiquity Powerbeam 5AC GEN2 → max 8.5W
- Ubiquity NanoBeam 5AC GEN2 → max 8.5W
Example total power consumption:
For this example we will try to estimate the total power consumption of a remote and solar powered LoRaWAN site with two Point-to-Point links.
- Mikrotik wAP LR8 → 5W → @24hours = 120 Wh per day
- Ubiquity EdgeSwitch ES-8 150W → 5W → @24hours = 120 Wh per day
- Ubiquity Powerbeam 5AC GEN2 → max 8.5W → @24hours = 204 Wh per day
- Ubiquity NanoBeam 5AC GEN2 → max 8.5W → @24hours = 204 Wh per day
The total power consumption for this LoRaWAN site is estimated at 27W → @24hours = 648 Wh per day
¶ Battery capacity
Battery specs:
Lithium-Ion battery packs:
- 6S16P LC18650
- Cells: INR18650-30Q
- Voltage: 22.2 V
- Capacity: 40 Ah / 1066 Wh
- 6S16P PANASONIC NCR
- Cells: NCR18650B
- Voltage: 22.2 V
- Capacity: 54.4 Ah / 1208 Wh
- 4S15P PANASONIC NCR
- Cells: NCR18650B
- Voltage: 14.8 V
- Capacity: 51 Ah / 755 Wh
- Victron - Lithium-iron-phosphate (LiFePO4 or LFP) Batteries Smart
- Example: LFPSmart 12,8/100
- Voltage: 12.8 V
- Capacity: 100 Ah / 1280 Wh
Portable Battery packs:
- Voltaic Systems - V88 Portable Laptop Battery + USB-C PD
- Cells: Li-Polymer
- Voltage: 12V/6A, 16V/5A, 19V/4.5A, 24V/3.5A
- Capacity: 24 Ah / 88.8 Wh
- Voltaic Systems - V250 Portable Laptop Battery + USB-C PD
- Cells: Li-Ion
- Voltage: 12V/6A, 16V/5A, 19V/4.5A, 24V/3.5A
- Capacity: 67.2 Ah / 246.6 Wh
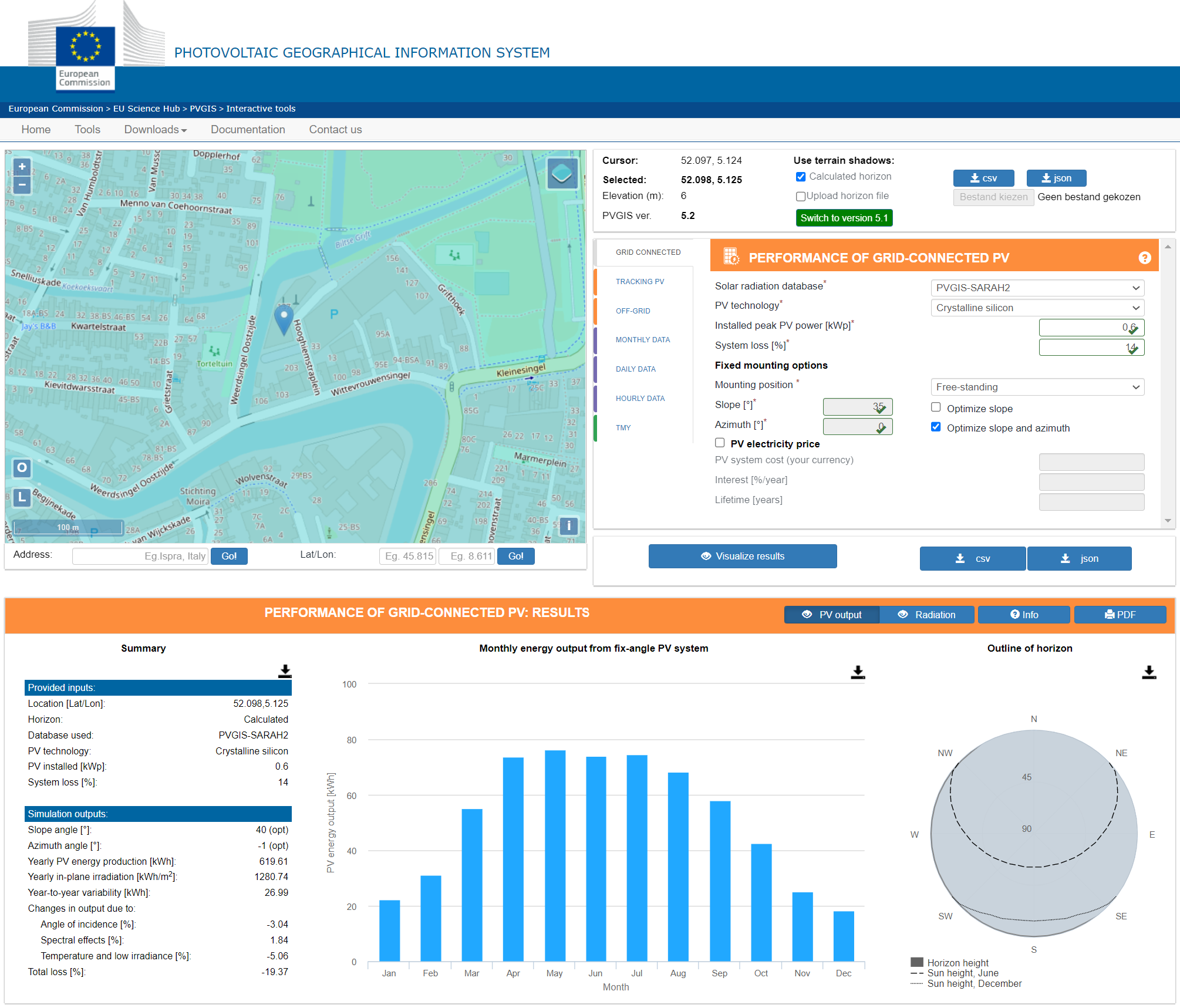
¶ Solar capacity
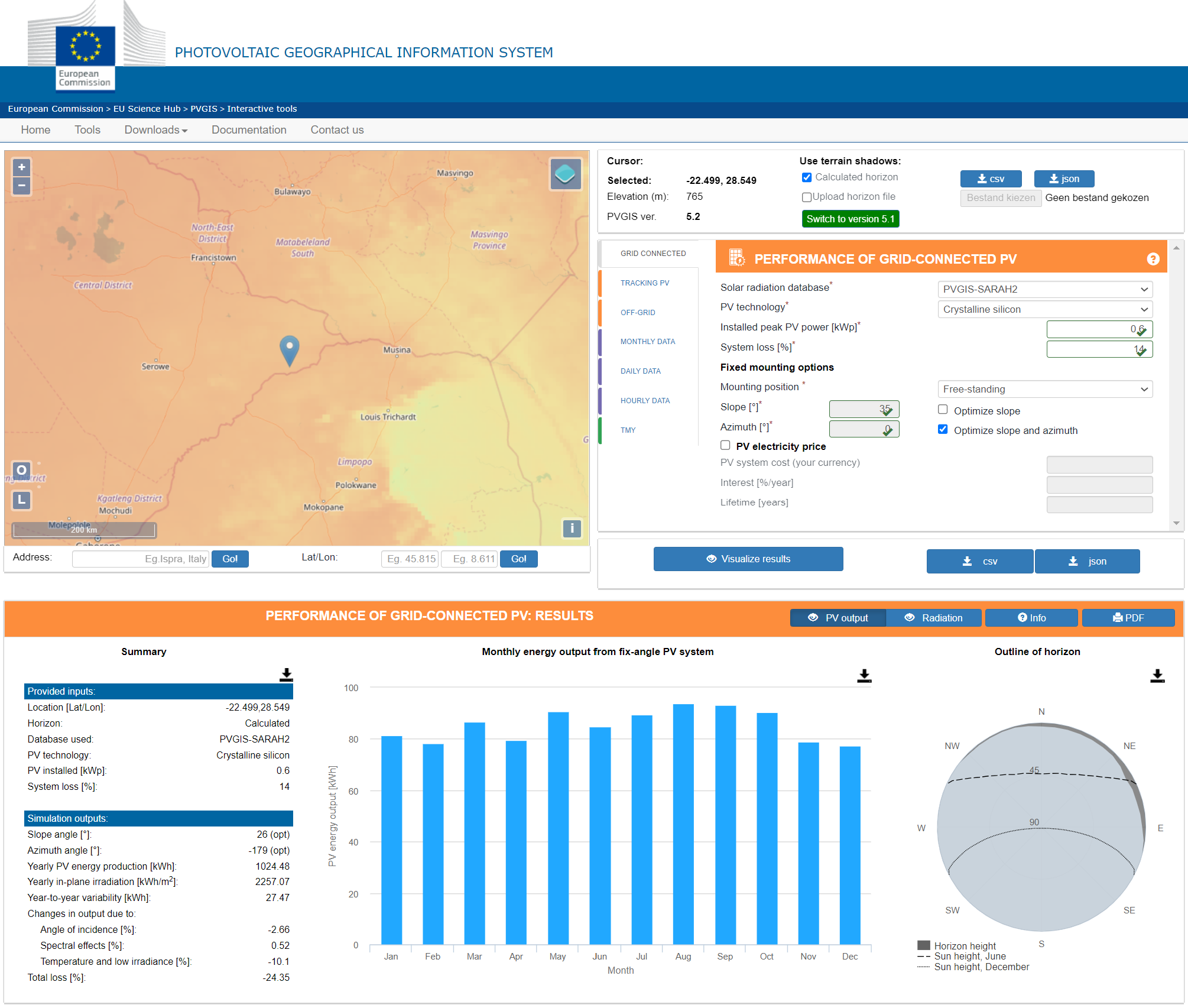
- Tool to calculate expected energy generated from your solar installation: https://re.jrc.ec.europa.eu/pvg_tools/en/tools.html
- Use the Grid Connect module: this tool will present you with the monthly energy generated by your setup for a given location.
- Location: use your cursor to place a point on the map to be used by the tool to calculate.
- Installed peak PV power (kWp): When you have 2 solar panels of 300 Wp, then 2 x 300 = 600 Wp = 0.6 kWp.
- Mounting position: Free-standing or Roof added /Building integrated → When the panels are placed in the field use Free-standing.
- Slope: to find the most optimal slope, please use the “Optimize slope and azimuth” checkbox → the tool will provide the most optimale slope.
- Azimuth: to find the most optimal azimuth, please use the “Optimize slope and azimuth” checkbox → the tool will provide the most optimale azimuth.
- Visualize results: → this button will generate a very useful graph with the following key details:
- Ideal (or given) slope angle
- Ideal (or given) azimuth angle
- Monthly energy output from fix-angle PV system → looking at the worst month, this will give you a good indication of what you can power from this set-up if it needs to run continuously all year long. The examples below will show the huge difference per location on earth.
Example 1 : Europe - The Netherlands
- Installed peak PV power (kWp): 2 x 300 Wp = 600 Wp = 0,6 kWp
- Ideal (or given) slope angle = 40°
- Ideal (or given) azimuth angle = 1°
- Monthly energy output from fix-angle PV system:
- Worst case = December @ 18.21 kWh → Day @ 587.42 Wh → Hour @ 24.48 Wh
- Best month = May @ 76.42 kWh
Example 2 : Africa - Botswana
- Installed peak PV power (kWp): 2 x 300 Wp = 600 Wp = 0,6 kWp
- Ideal (or given) slope angle = 26°
- Ideal (or given) azimuth angle = 179°
- Monthly energy output from fix-angle PV system:
- Worst month = December @ 77.29 kWh → Day @ 2.49 kWh → Hour @ 103.88 Wh
- Best month = August @ 93.74 kWh